AVX2 32-member indexing set
|#
Appendix
In this article, I propose a 32 (or more) element indexing set
as well as an AVX2 implementation. The complexity of both insertion
and deletion is O(n*k), where
n is the number of elements and
k is their size in bytes.
This structure was optimized for fast finding as it's used in a
Misra–Gries heavy hitters algorithm
implementation.
struct CSet32 {
__m256i vec[3];
uint32_t valmask = 0;
};
While at first this design approach may seem naive, we can leverage SIMD to cut down our constant factors tremendously. With a simple observation, we can notice that finding the index at which an element resides is as simple as testing its bytes of for equality with all of the currently stored values. As it turns out, this is an area where SIMD shines because we can compare multiple values at once.
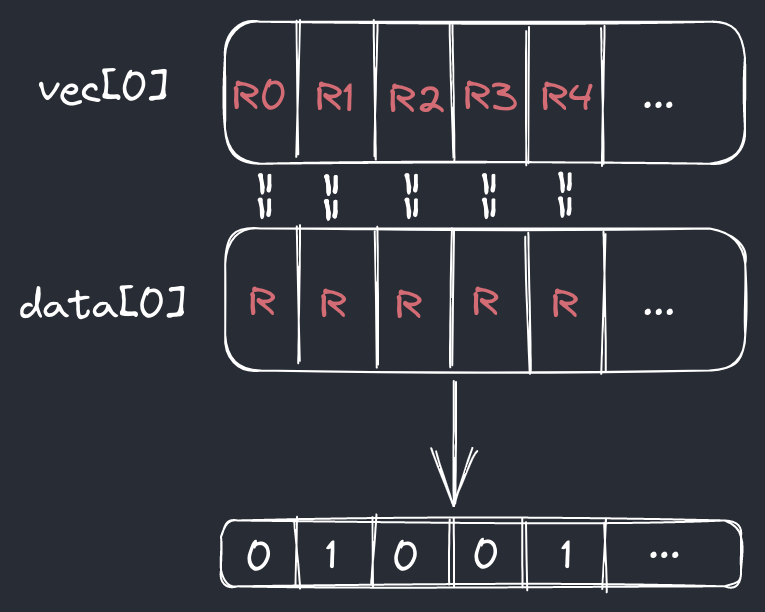
Let's take a look at how one would implement it in c++ using intrinsics:
int find(uint8_t* data) {
int res;
__m256i acc;
__m256i mask[3];
for (size_t i = 0; i < 3; i++)
mask[i] = _mm256_set1_epi8(data[i]);
acc = _mm256_cmpeq_epi8(mask[0], vec[0]);
for (size_t i = 1; i < 3; i++)
acc = _mm256_and_si256(acc, _mm256_cmpeq_epi8(mask[i], vec[i]));
res = _mm256_movemask_epi8(acc);
res &= valmask;
return (res ? __builtin_ctz(res) : 32);
}
It's not as trivial as the picture shows as we have to AND with
valmask which denotes the set elements
as bits turned on in a 32 bit integer and then find the index of the
set bit using __builtin_ctz()
(if such bit exists) as otherwise we return 32 which denotes an invalid value.
And here is the assembly codegen by clang 15, annotated by me:
.cset32_find: ; @cset32_find(CSet32*, unsigned char*)
; mask[0] = _mm256_set1_epi8(data[0])
vpbroadcastb ymm0, byte ptr [rsi]
; mask[1] = _mm256_set1_epi8(data[1])
vpbroadcastb ymm1, byte ptr [rsi + 1]
; mask[2] = _mm256_set1_epi8(data[2])
vpbroadcastb ymm2, byte ptr [rsi + 2]
; acc = _mm256_cmpeq_epi8(mask[0], vec[0])
vpcmpeqb ymm0, ymm0, ymmword ptr [rdi]
; acc = _mm256_and_si256(acc, _mm256_cmpeq_epi8(mask[1], vec[1]))
vpcmpeqb ymm1, ymm1, ymmword ptr [rdi + 32]
vpand ymm0, ymm1, ymm0
; acc = _mm256_and_si256(acc, _mm256_cmpeq_epi8(mask[2], vec[2]))
vpcmpeqb ymm1, ymm2, ymmword ptr [rdi + 64]
vpand ymm0, ymm0, ymm1
; res = _mm256_movemask_epi8(acc);
vpmovmskb eax, ymm0
; res &= valmask;
and eax, dword ptr [rdi + 96]
je .BSF_FAIL
; return __builtin_ctz(res)
bsf eax, eax
vzeroupper
ret
.BSF_FAIL:
; return 32
mov eax, 32
vzeroupper
ret
With find() done, implementing
insertions will be just as easy as we have to find the first free spot
in our valmask by computing ctz(~valmask)
which yields the index of the first not set bit and then just change
singular bytes in the vectors respectively.
int insert(uint8_t* data) {
int idx = find(data);
int free_idx;
if (idx != 32) return idx;
free_idx = __builtin_ctz(~valmask);
uint8_t cbuf[32] __attribute__((aligned(32)));
for (size_t i = 0; i < 3; i++) {
_mm256_store_si256((__m256i*)cbuf, vec[i]);
cbuf[free_idx] = data[i];
vec[i] = _mm256_load_si256((__m256i*)cbuf);
}
valmask |= (1<<free_idx);
return free_idx;
}
The code above also contains checks for duplicates as well as not the most efficient way of setting singular bytes in a vector register.
.cset32_insert: ; @cset32_insert(CSet32*, unsigned char*)
push rbp
mov rbp, rsp
push r14
push rbx
; stack alignment
and rsp, -32
sub rsp, 32
mov r14, rsi
mov rbx, rdi
call CSet32::find(unsigned char*)
cmp eax, 32
jne .FIND_SUCC ; if (idx != 32) return idx
mov ecx, dword ptr [rbx + 96] ; valmask
mov eax, ecx
not eax
bsf eax, eax ; __builtin_ctz(~valmask)
; i = 0
vmovaps ymm0, ymmword ptr [rbx]
vmovaps ymmword ptr [rsp], ymm0
movzx edx, byte ptr [r14]
mov byte ptr [rsp + rax], dl
vmovaps ymm0, ymmword ptr [rsp]
vmovaps ymmword ptr [rbx], ymm0
; i = 1
vmovaps ymm0, ymmword ptr [rbx + 32]
vmovaps ymmword ptr [rsp], ymm0
movzx edx, byte ptr [r14 + 1]
mov byte ptr [rsp + rax], dl
vmovaps ymm0, ymmword ptr [rsp]
vmovaps ymmword ptr [rbx + 32], ymm0
; i = 2
vmovaps ymm0, ymmword ptr [rbx + 64]
vmovaps ymmword ptr [rsp], ymm0
movzx edx, byte ptr [r14 + 2]
mov byte ptr [rsp + rax], dl
vmovaps ymm0, ymmword ptr [rsp]
vmovaps ymmword ptr [rbx + 64], ymm0
btc ecx, eax
mov dword ptr [rbx + 96], ecx
.FIND_SUCC:
lea rsp, [rbp - 16]
pop rbx
pop r14
pop rbp
vzeroupper
ret
*Call to find() was not inlined as
that would make the output even bigger than it's now.
With that out of the way, the rest of operations (size, clear, remove) are trivial to implement so their details won't be mentioned here. Complete implemention below:
#include <immintrin.h>
#include <stdint.h>
struct CSet32 {
__m256i vec[3];
uint32_t valmask = 0;
inline int size() { return __builtin_popcount(valmask); }
inline int find(uint8_t* data) {
int res;
__m256i acc;
__m256i mask[3];
for (size_t i = 0; i < 3; i++)
mask[i] = _mm256_set1_epi8(data[i]);
acc = _mm256_cmpeq_epi8(mask[0], vec[0]);
for (size_t i = 1; i < 3; i++)
acc = _mm256_and_si256(acc, _mm256_cmpeq_epi8(mask[i], vec[i]));
res = _mm256_movemask_epi8(acc);
res &= valmask;
return (res ? __builtin_ctz(res) : 32);
}
inline int insert(uint8_t* data) {
int idx = find(data);
int free_idx;
if (idx != 32) return idx;
free_idx = __builtin_ctz(~valmask);
uint8_t cbuf[32] __attribute__((aligned(32)));
for (size_t i = 0; i < 3; i++) {
_mm256_store_si256((__m256i*)cbuf, vec[i]);
cbuf[free_idx] = data[i];
vec[i] = _mm256_load_si256((__m256i*)cbuf);
}
valmask ^= (1<<free_idx);
return free_idx;
}
inline int insert_at(int idx, uint8_t* data) {
uint8_t cbuf[32] __attribute__((aligned(32)));
for (size_t i = 0; i < 3; i++) {
_mm256_store_si256((__m256i*)cbuf, vec[i]);
cbuf[idx] = data[i];
vec[i] = _mm256_load_si256((__m256i*)cbuf);
}
valmask |= (1<<idx);
return idx;
}
inline bool present_at(int idx) {
return valmask & (1<<idx);
}
inline void remove(uint8_t* data) {
int idx = find(data);
valmask ^= (1<<idx);
}
inline void remove_at(int idx) {
valmask ^= (1<<idx);
}
inline void clear() {
valmask = 0;
}
};
#
Conclusions
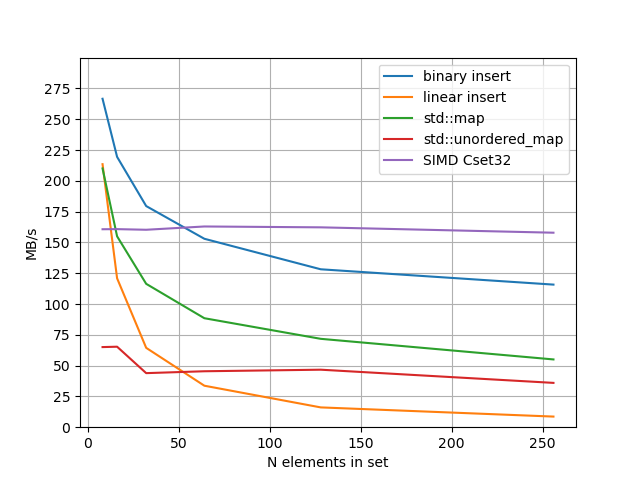
As we can see, misra-gries algorithm using the (extended) SIMD map
performs the same no matter the number of nonempty buckets and
outperforms the both std::map and std::unordered_map by a minimum
factor of 3.
If you've found this useful, you might wanna check out my other articles and my twitter. Please let me know about any mistakes I've made here in the comments below.
< Previous |




